Efektivita programů

Při programování je důležité určit míru efektivity algoritmu a případné kroky pro jeho optimalizaci. Mohlo by se zdát, že nejlepším řešením, jak zjistit, jak je program rychlý je změřit čas spuštění a čas ukončení programu a ty od sebe odečíst. Tím, ale je možné zjistit, jen jak se program chová pro jeden konkrétní vstup na jednom konkrétním zařízení. Poměrně běžně se pak stává, že lokálně na počítači vývojáře se zdá řešení efektivní, nicméně po nasazení do produkčního prostředí dochází ke zjištění, že je výpočet pomalý.

Ukázka

Následující program provede součet celých čísel { 1, 2, … 10 }.

int result = 0;
int min = 1;
int max = 10;
 
for (int i = min; i <= max; i++)
{
    result += i;
}

Otázka: Kolikrát musí proběhnout cyklus? Čísla se sčítají postupně a celkem čísel je 10, takže desetkrát. U této úlohy je však otázkou, jestli na tento problém je vhodné psát program, protože výsledek bude vždy stejný.

Co když ale horní mez nebude nastavena staticky, ale může ji zvolit uživatel programu. Kolikrát pak program proběhne? No tolikrát, jak je veliký vstup.

int result = 0;
int min = 1;
 
if(!int.TryParse(Console.ReadLine(), out int max))
{
    Console.WriteLine("Nesprávný vstup");
    return;
}
 
for (int i = min; i <= max; i++)
{
    result += i;
}

Kdy efektivitu řešit?

V případě, že vstup programu je malého rozsahu, tak neoptimální a optimální řešení bude dosahovat velmi podobných výsledků. Pokud se ale začne zvětšovat vstup, tak optimální řešení může být rychlejší o stovky i tisíce procent.

Asymptotická časová složitost

V praxi se často stává, že je nutné optimalizovat nějaký kód a tím vznikají dvě verze algoritmu, které řeší ten stejný problém. Tyto verze je následně potřebné porovnat a určit, která je rychlejší. Co ale znamená, že je rychlejší? To je nutné formalizovat.

Typy složitosti

• Časová složitost – doba výpočtu, která je potřebná pro vyřešení daného problému
• Paměťová složitost – velikost paměti, která je potřebná pro provedení výpočtu

Asymptotická složitost jako matematická funkce

Každému algoritmu lze jednoznačně přiřadit neklesající funkci, která charakterizuje počet jeho operací v závislosti na rostoucí velikosti vstupních dat.

U této funkce je klíčové, že je možné ignorovat konstanty a také, že je vždy nejdůležitější člen s nejvyšším řádem. Tedy pokud má algoritmus časovou složitost $3n^2+7n+8$, tak to lze zjednodušit na $n^2$. To znamená tedy, že asymptotická mez je přibližná mez.

Dále platí i to, že každý problém lze sestavit ve větší časové složitosti (hůře to jde udělat vždy), ale naopak každý problém má minimální časovou a paměťovou složitost, pod kterou jej nelze vyřešit. Tuto mez lze pomocí matematických metod i dokázat.

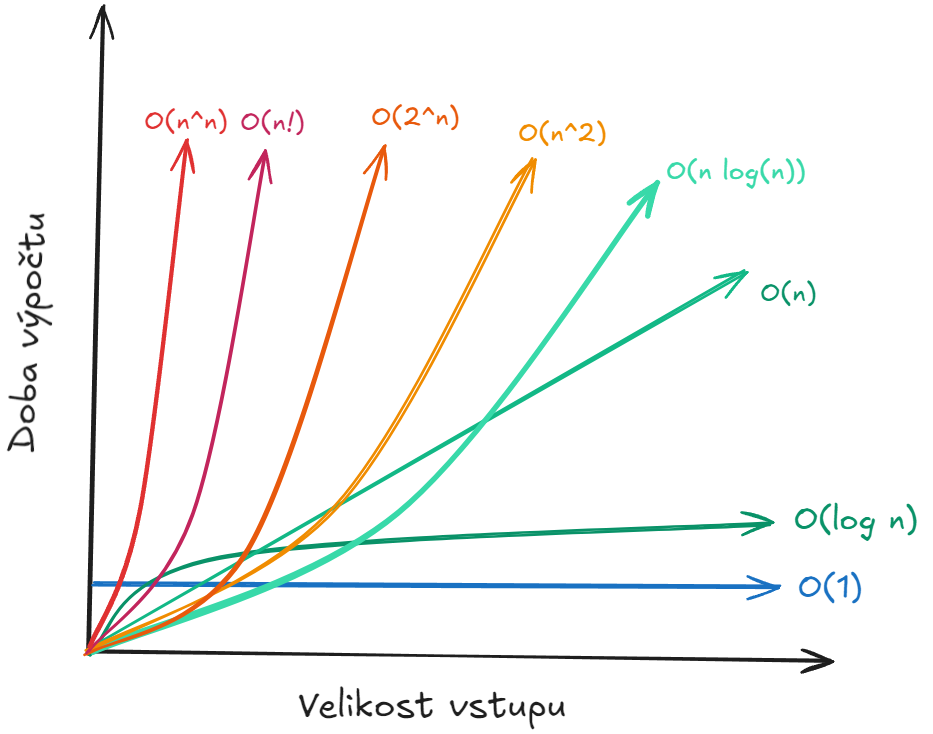
Notace velké $\mathcal{O}$

Určuje horní mez složitosti algoritmu.

Zápis	Název	Příklad algoritmu
$\mathcal{O}(1)$	konstantní	Přístup k prvku v poli
$\mathcal{O}(logn)$	logaritmická	Binární vyhledávání
$\mathcal{O}(n)$	lineární	Procházení seznamu
$\mathcal{O}(nlogn)$	lineárně-logaritmická	Efektivní řadící algoritmy (merge sort, quick sort průměrně)
$\mathcal{O}(n^2)$	kvadratická	Vnořené smyčky (například bubble sort)
$\mathcal{O}(2^n)$	exponenciální	Rekurzivní řešení problému obchodního cestujícího
$\mathcal{O}(n!)$	faktoriální	Hrubou silou generování permutací

Asymptotické notace

Značka	Název	Popis	Slovně
$\mathcal{O}(f(n))$	Horní mez (Upper Bound)	Algoritmus nebude horší než $f(n)$ pro dostatečně velké $n$	„nejhůře roste jako“
$o(f(n))$	Horní mez nevčetně	Algoritmus roste pomaleji než $f(n)$	„roste pomaleji než“
$\Omega (f(n))$	Dolní mez (Lower Bound)	Algoritmus bude nejméně tak rychlý jako $f(n)$	„nejméně roste jako“
$\omega (f(n))$	Dolní mez nevčetně	Algoritmus roste rychleji než $f(n)$	„roste rychleji než“
$\Theta (f(n))$	Střední mez (Theta)	Algoritmus roste přesně jako $f(n)$ – horní i dolní mez shodné	„roste přibližně jako“

Ukázka asymptotické časové a prostorové složitosti algoritmu

V rámci příkladu je vytvořena kolekce DynamicArray, která reprezentuje dynamické pole, které mění svou velikost dle počtu prvků. Na kolekci jsou definovány operace:

• Add - přidání prvku na první volné místo v kolekci
• Remove - odebrání prvku z indexu a zarovnání kolekce doleva tak, aby prvky tvořily souvislý blok.
• Get - získání prvku na indexu

Ukázka

using System;
 
public class DynamicArrayArray
{
    private int[] data;
    private int count;
 
    public DynamicArrayArray()
    {
        data = new int[4]; // počáteční kapacita
        count = 0;
    }
 
    public void Add(int value)
    {
        if (count == data.Length)
        {
            // zvětšit pole (například 2x větší)
            int newCapacity = data.Length * 2;
            int[] newData = new int[newCapacity];
            Array.Copy(data, newData, data.Length);
            data = newData;
        }
 
        data[count] = value;
        count++;
    }
 
    public int Get(int index)
    {
        if (index < 0 || index >= count)
            throw new IndexOutOfRangeException();
 
        return data[index];
    }
 
    public void Remove(int index)
    {
        if (index < 0 || index >= count)
            throw new IndexOutOfRangeException();
 
        // posun zbylých prvků vlevo
        for (int i = index; i < count - 1; i++)
        {
            data[i] = data[i + 1];
        }
        count--;
    }
 
    public int Count => count;
}
 

Prostorová složitost

Je nutné uložit $n$ prvků (resp. při zvětšování pole je potřebná velikost $2n$, ale konstanta se zanedbává). Není potřeba žádná paměť navíc, takže je asymptotická paměťová složitost $\mathcal{O}(n)$.

Časová složitost

1. Get(index)

int value = array.Get(i);

• je to přístup do pole
• známe index prvku, tedy jen získáme data na indexu. To lze udělat v konstantním čase, tj. $\mathcal{O}(1)$

→ žádné prohledávání, žádné cykly

2. Remove(index)

array.Remove(i);

• prvky na indexech větší než i se musí všechny posunout o jedno doleva
  • Takovýchto prvků může být maximálnět $n-1$ tj. $\mathcal{O}(n)$ v nejhorším případě

Příklad:

0	1	2	3
10	20	30	40

• odeber index 1 (20)
• posune se 30 na místo 20, 40 na místo 30

Tedy:

• Remove na začátku → $\mathcal{O}(n)$
• Remove na konci → $\mathcal{O}(1)$

→ průměrně $\mathcal{O}(n)$

3. Add(value)

if (count == data.Length)
{
    int newCapacity = data.Length * 2;
    int[] newData = new int[newCapacity];
    Array.Copy(data, newData, data.Length);
    data = newData;
}
 
data[count] = value;
count++;

Dvě situace dle kapacity:

• Kapacita stačí - Hodnota se uloží za $\mathcal{O}(1)$
• Kapacita nestačí - Zkopírování $n$ prvků → $\mathcal{O}(n)$ a přidání jednoho prvku $\mathcal{O}(1)$

Amortizovaná časová složitost je $\mathcal{O}(1)$. Tzn. limitně, kdy počet prvků jde do nekonečna, trvá přidání jednoho prvku konstantní čas.