Kostra grafu

Kostra grafu (anglicky spanning tree) je takový podgraf neorientovaného grafu, který:

• obsahuje všechny vrcholy původního grafu,
• je souvislý (existuje cesta mezi libovolnou dvojicí vrcholů),
• neobsahuje žádný cyklus.

Pokud graf $G$ obsahuje $n$ vrcholů, pak každá jeho kostra obsahuje přesně $n-1$ hran.

Nalezení kostry je klíčové v úlohách, kde je třeba propojit všechny uzly s minimálními náklady:

• návrh komunikačních sítí (telefonní, počítačové),
• stavba dopravních sítí,
• optimalizace elektrických rozvodů,
• algoritmy pro shlukování dat (například v datové analýze).

Kostra vs. Minimální kostra

Pokud je graf:

• neohodnocený – všechny kostry jsou si rovnocenné.
• ohodnocený – je potřeba najít takovou kostru, která má nejnižší možný součet vah hran. Taková kostra se nazývá Minimální kostra (Minimum Spanning Tree)

Důležité vlastnosti:

• Minimální kostra existuje, pokud je graf souvislý.
• Minimální kostra nemusí být jednoznačná – různé podgrafy mohou mít stejnou minimální váhu.

Algoritmy pro nalezení minimální kostry

Pro nalezení kostry existují tři základní algoritmy:

• Jarníkův (Primův)
• Kruskalův
• Borůvkův

Jarníkův algoritmus (Primův algoritmus)

• Začíná v libovolném vrcholu.
• Postupně vybírá nejlevnější hranu, která spojuje již vybranou množinu vrcholů se zbytkem grafu.
• Přidá vrchol do kostry a proces opakuje.

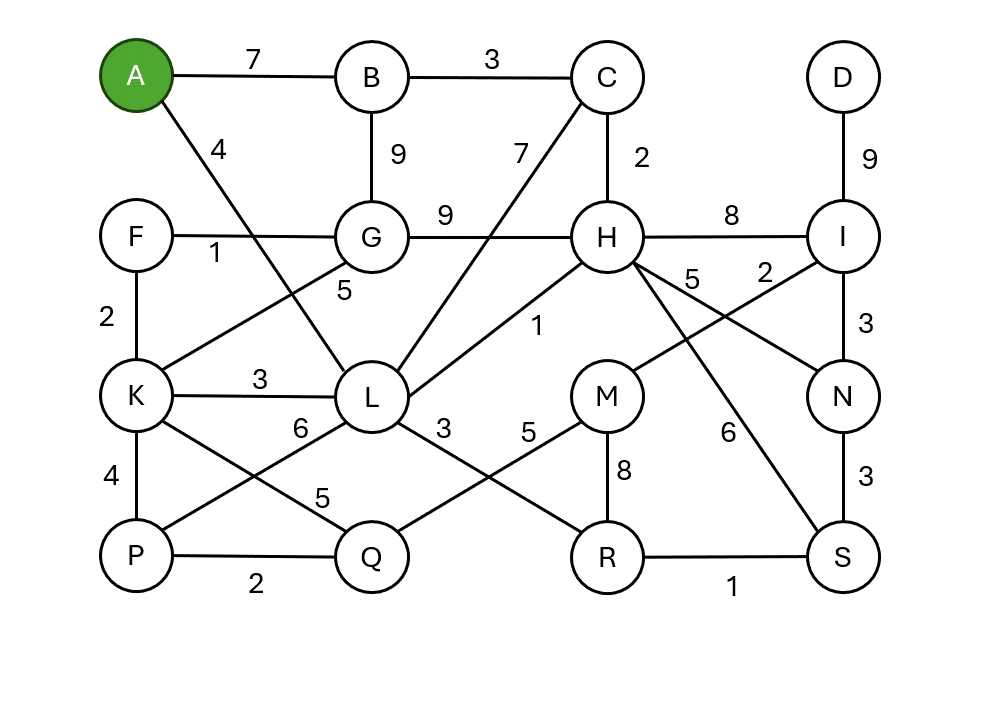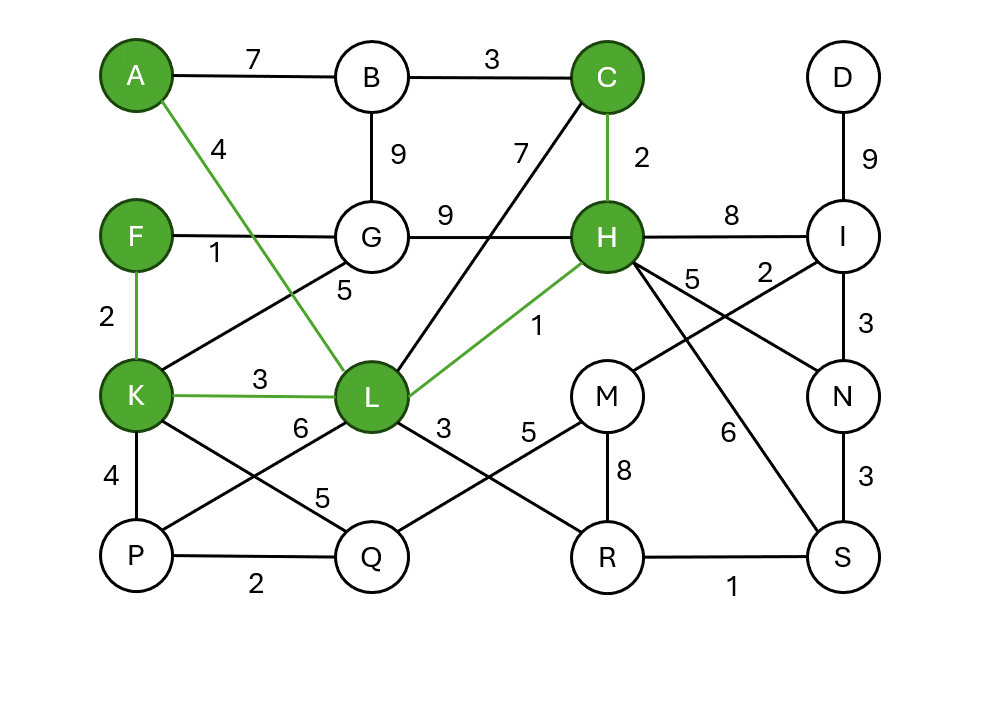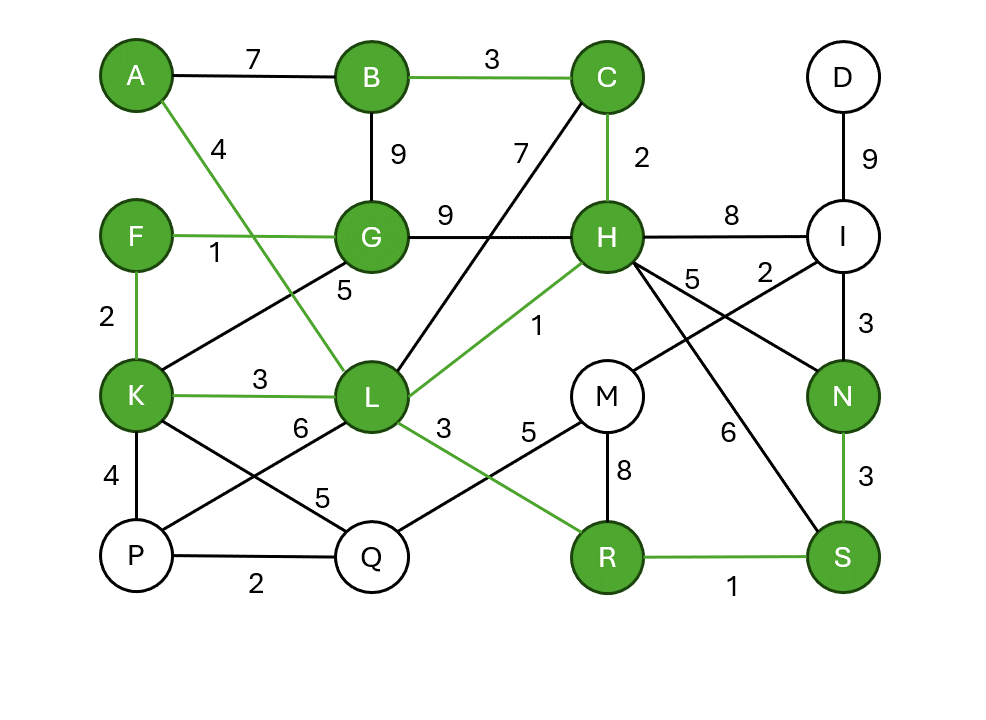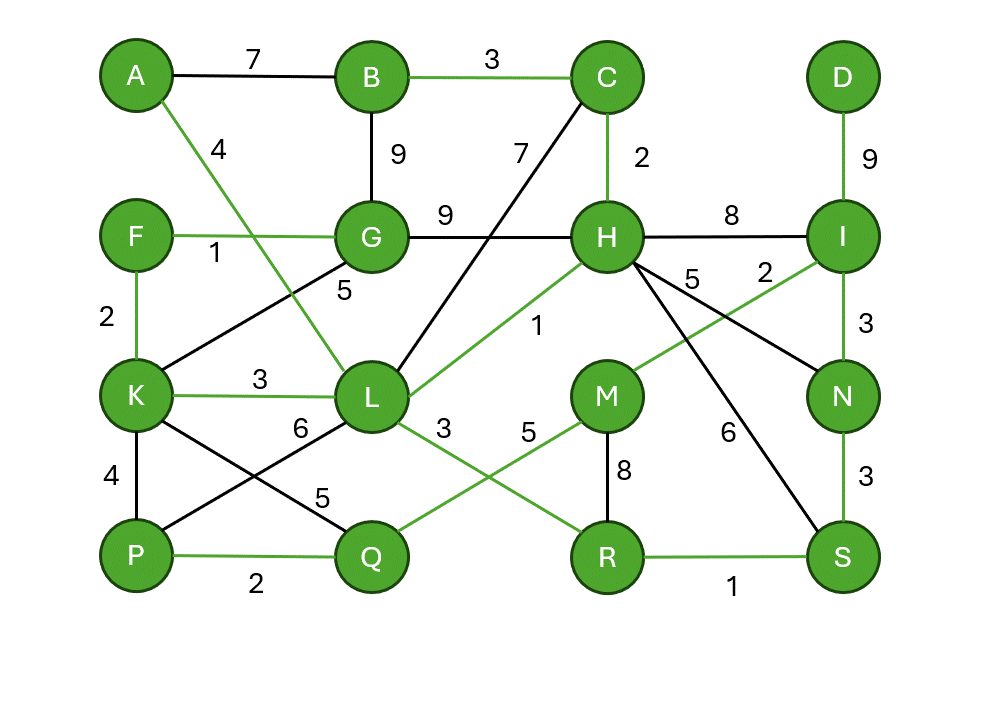
Pseudokód

Prim(G):
    MST = {}
    Start s libovolným vrcholem u
    Přidej u do MST
    Dokud existuje hrana z MST ven:
        vyber hranu (u,v) s minimální vahou
        pokud v není v MST:
            přidej hranu (u,v) do MST
            přidej v do MST

Časová složitost

• $\mathcal{O}(ElogV)$ při použití binární haldy.
• V hustých grafech může být rychlejší než Kruskal.

Prostorová složitost

• $\mathcal{O}(V+E)$ pro uložení grafu.
• $\mathcal{O}(V)$ pro frontu.

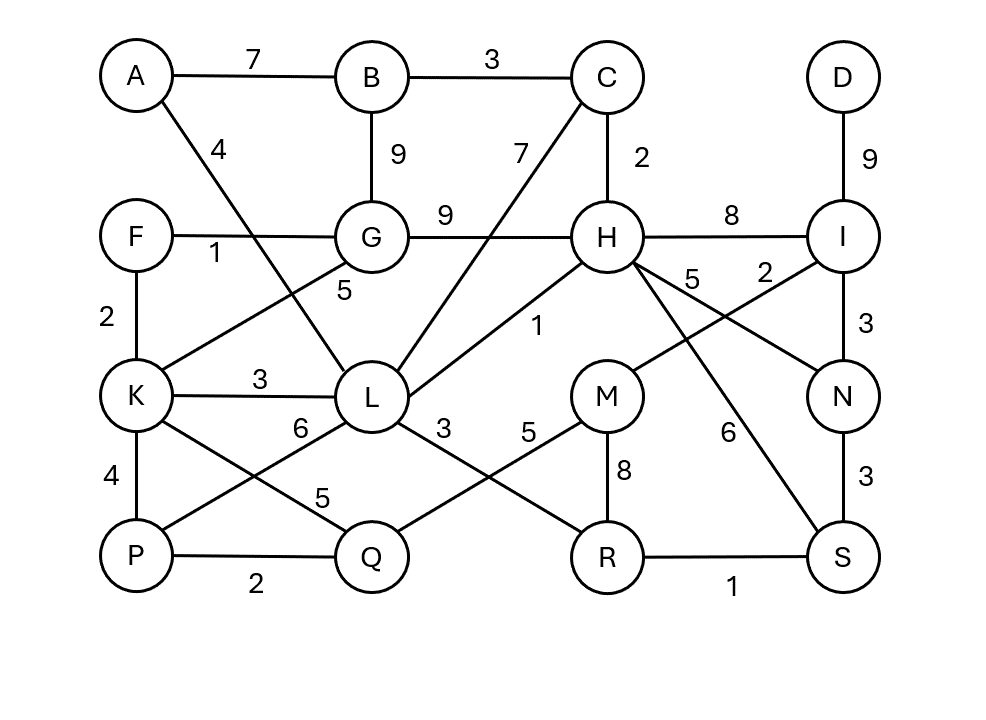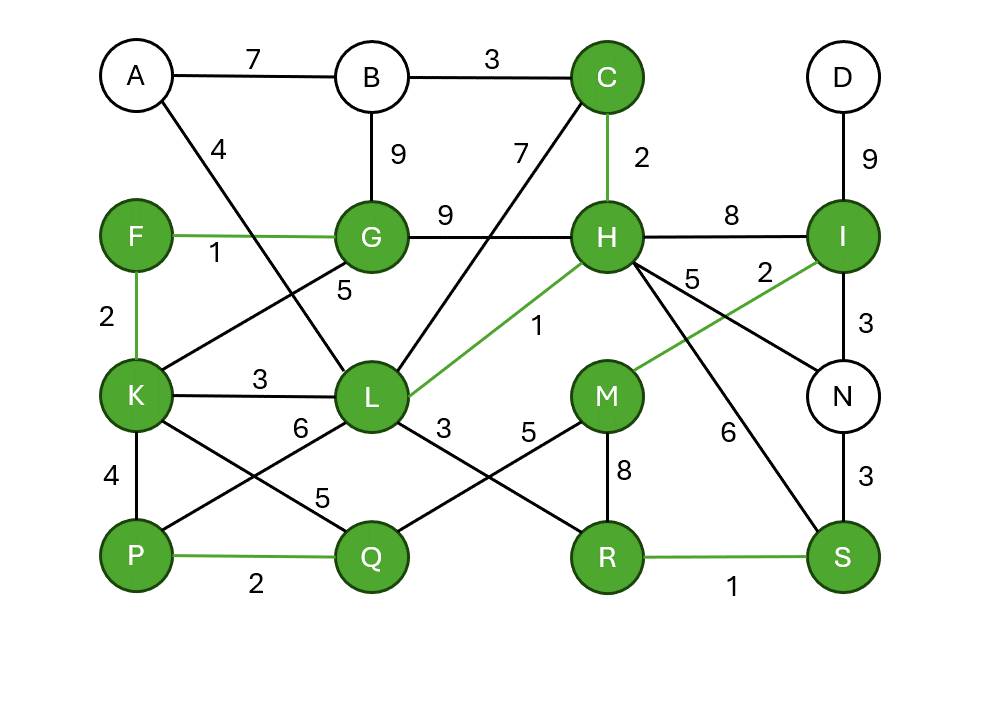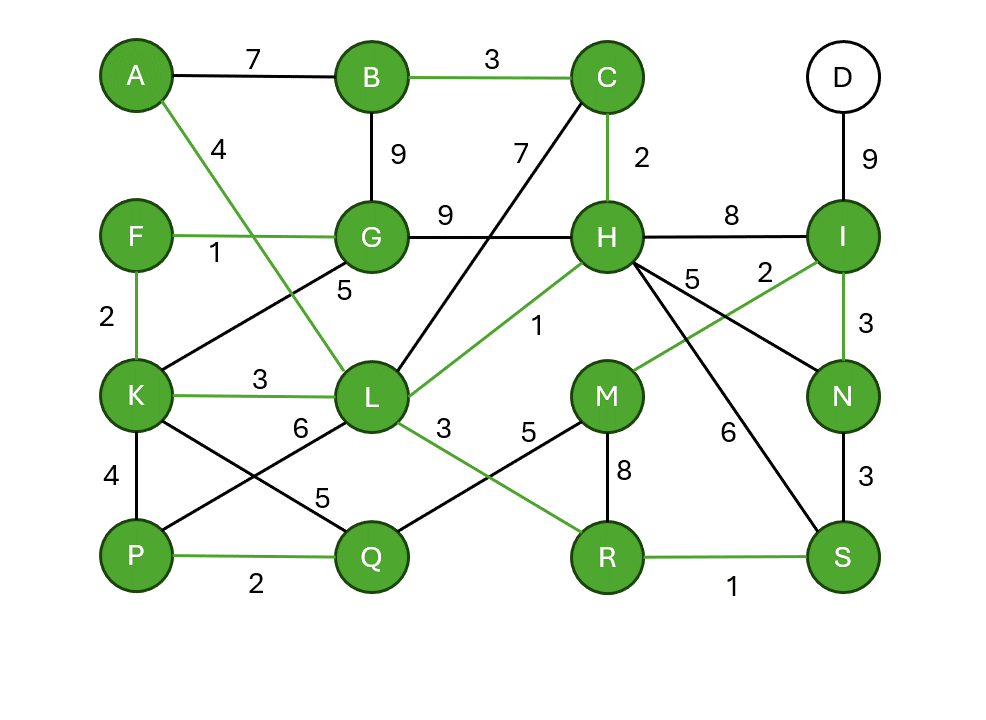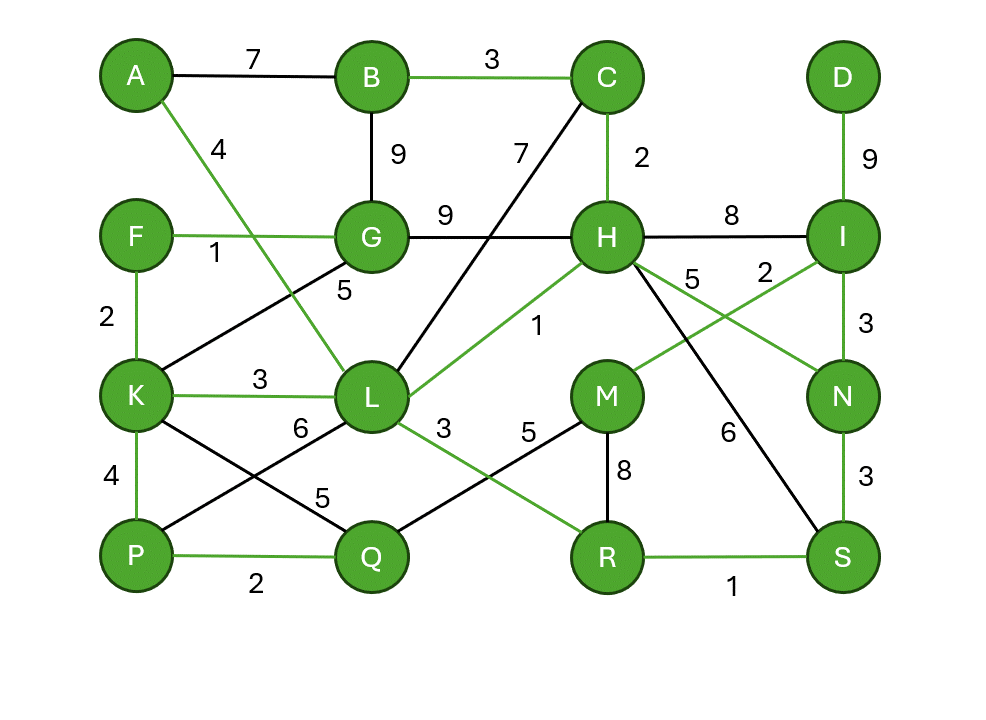
Kruskalův algoritmus

• Seřadí všechny hrany podle váhy.
• Prochází hrany od nejmenší váhy.
• Hranu přidá, pokud nespojuje již propojené komponenty (nevytváří cyklus).

Pseudokód

Kruskal(G):
    MST = {}
    seřaď všechny hrany podle vah
    foreach hrana (u,v) ve vzestupném pořadí:
        pokud u a v nejsou ve stejné komponentě:
            přidej (u,v) do MST
            slouč komponenty u a v

Časová složitost

• $\mathcal{O}(ElogE)$ na řazení hran.
• $\mathcal{O}(V)$ zbytek algoritmu

Prostorová složitost

• $\mathcal{O}(V+E)$

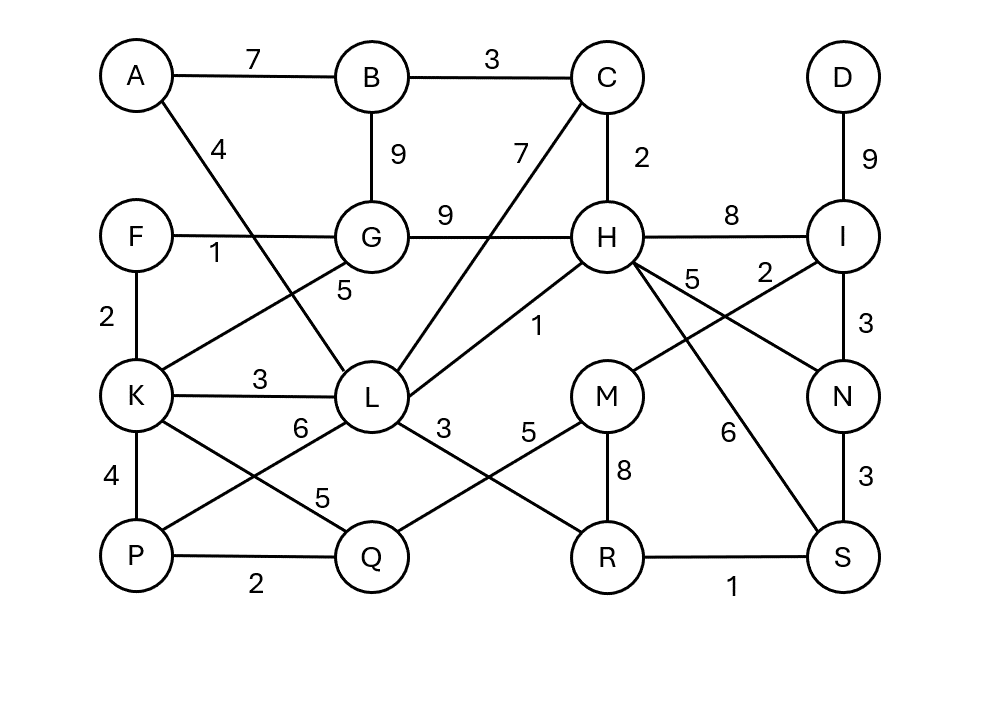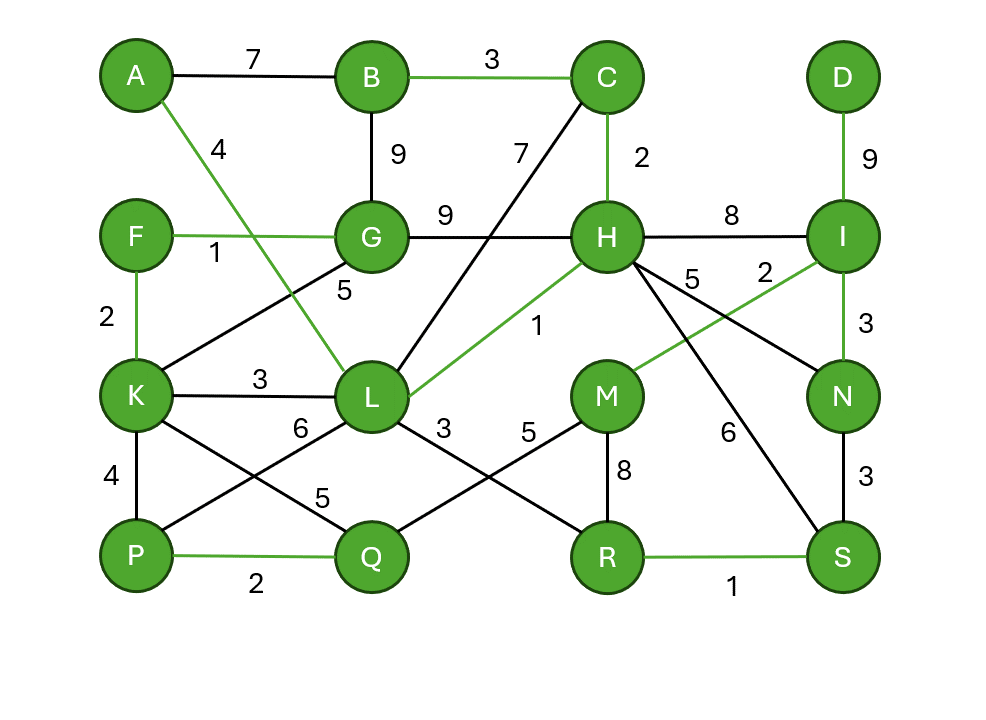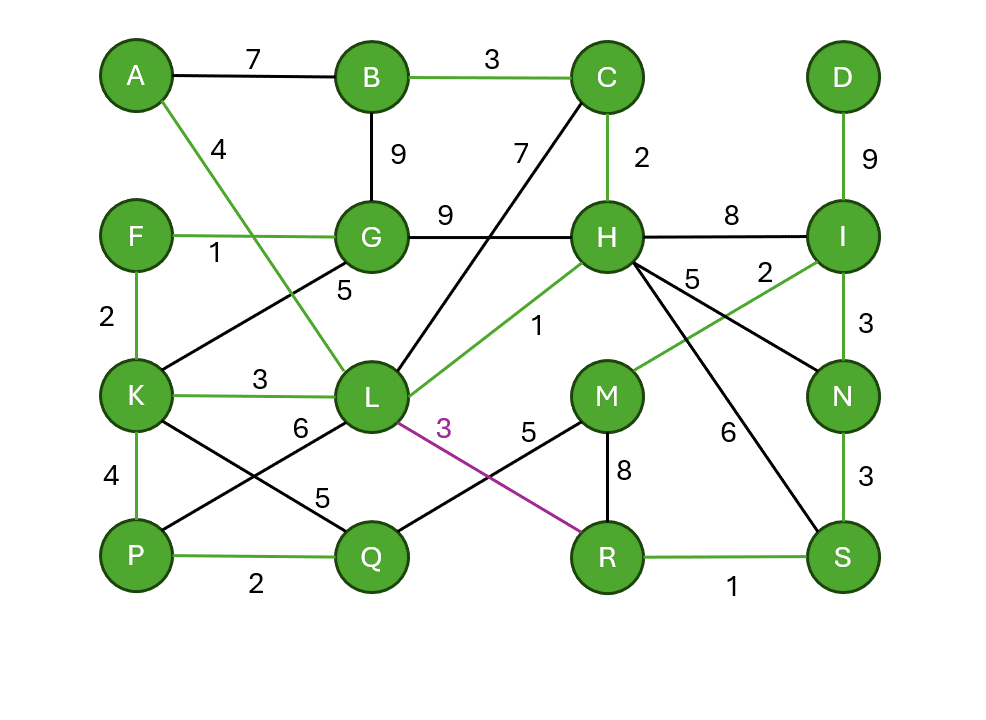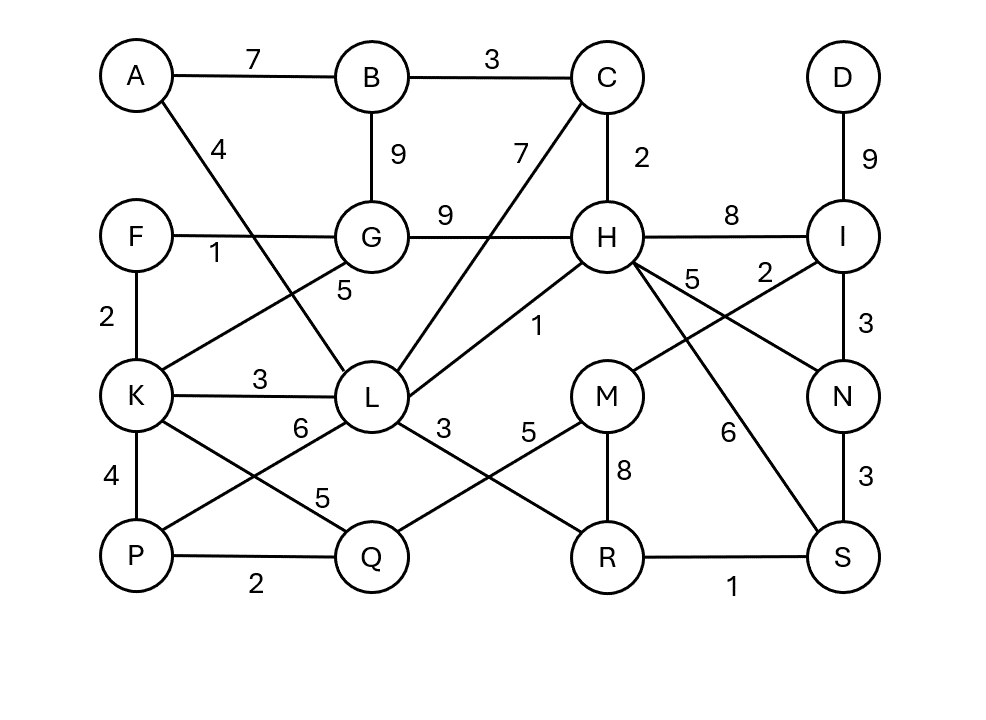
Borůvkův algoritmus

• Každý vrchol tvoří samostatnou komponentu souvislosti.
• Každá komponenta najde nejlevnější hranu ven.
• Všechny tyto hrany se přidají současně.
• Opakuje se, dokud není celý graf spojen do jedné komponenty.

Pseudokód

Boruvka(G):
    každému vrcholu přiřaď vlastní komponentu
    MST = {}
    while počet komponent > 1:
        pro každou komponentu C:
            najdi nejlevnější hranu (u,v) vycházející z C
        přidej všechny tyto hrany do MST
        slouč komponenty propojené nově přidanými hranami

Časová složitost

• $\mathcal{O}(ElogV)$
• Efektivní zejména v řídkých grafech, protože na každém kroku významně klesá počet komponent.

Prostorová složitost

• $\mathcal{O}(V+E)$