Reprezentace grafů v paměti

Reprezentace grafů v paměti

Graf lze v paměti uchovávat třemi základními způsoby. Každý z nich je vhodný pro různé typy úloh a má odlišné nároky na časovou a paměťovou složitost.

Způsoby uložení:

1. Matice sousednosti
2. Seznam sousedů
3. Seznam hran

Příklad grafu

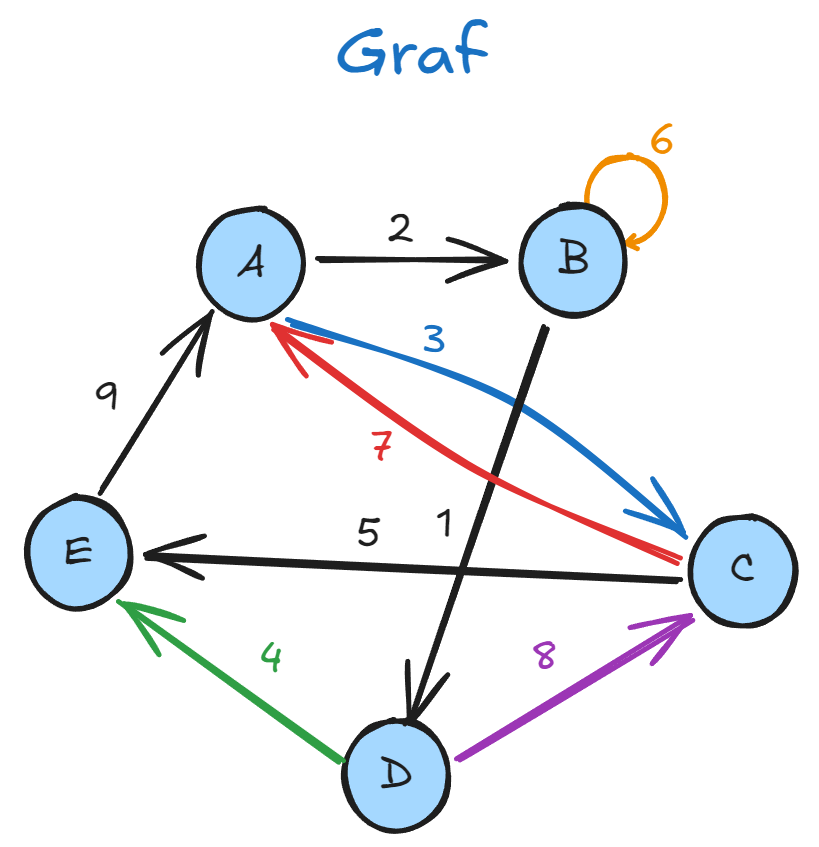
1. Matice sousednosti

Matice sousednosti je čtvercová matice $n\times n$, kde $n$ je počet vrcholů grafu.

• Prvek $A[i,j]$ indikuje existenci hrany mezi vrcholem $i$ a $j$.
• U neorientovaného grafu je matice symetrická, tedy $A[i,j]=A[j,i]$
• Přítomnost hrany se značí 1 a chybějící hrana se značí 0
• U ohodnoceného grafu matice obsahuje místo 0/1 přímo váhu hrany - případně 0, pokud hrana neexistuje

Výhody

• Rychlé ověření existence hrany $O(1)$
• Jednoduchá implementace

Nevýhody

• Paměťová náročnost $O(n^2)$ i u řídkých grafů
• Neefektivní při malém počtu hran vzhledem k počtu vrcholů

Příklad

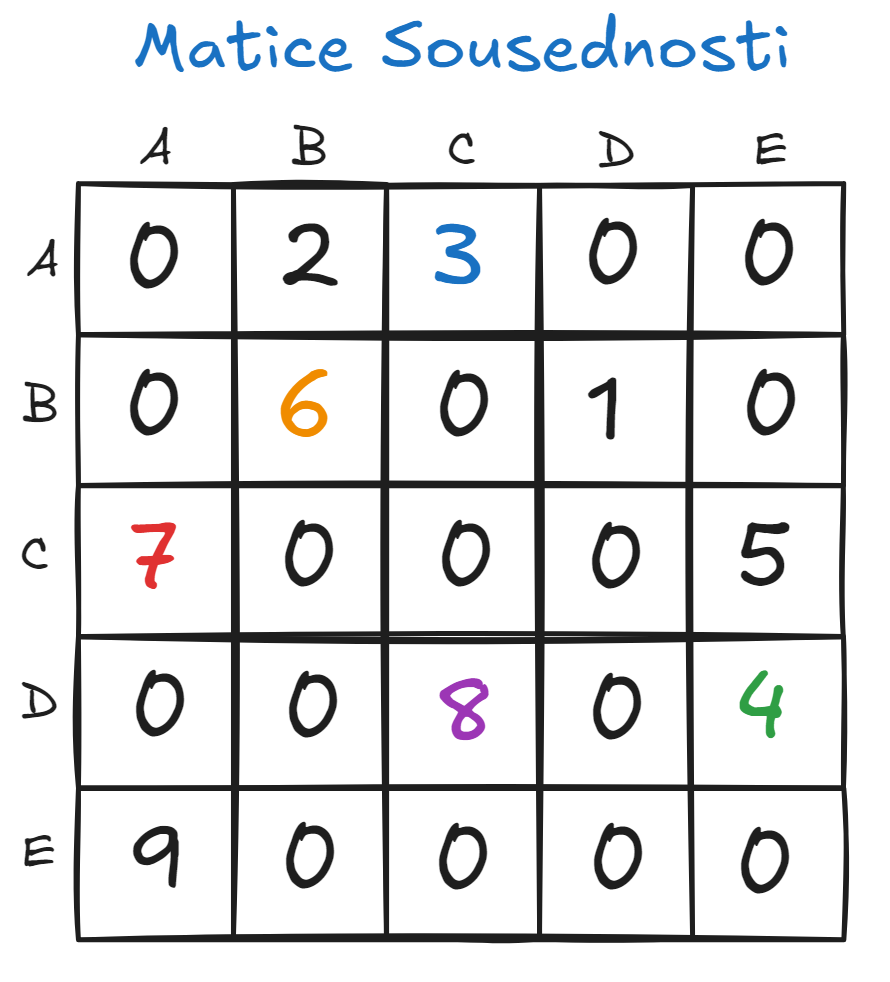
2. Seznam sousedů

Seznam sousedů ukládá ke každému vrcholu seznam vrcholů, do nichž vedou hrany.

Výhody

• Paměťová úspora u řídkých grafů $O(n+m)$, kde $m$ je počet hran
• Snadný průchod sousedy daného vrcholu

Nevýhody

• Ověření existence hrany může být až $O(\mathrm{deg}(v))$
• Složitější implementace některých algoritmů (např. hledání všech hran)

Příklad

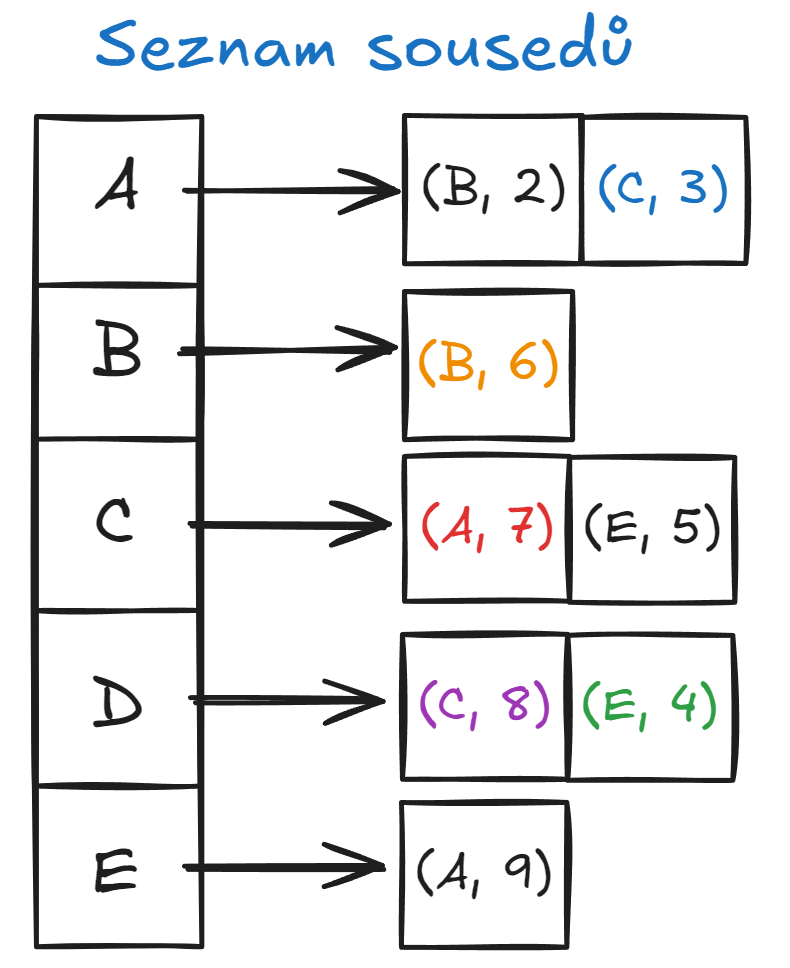
3. Seznam hran

Seznam hran ukládá graf jako prostý seznam dvojic (nebo trojic u ohodnocených grafů) reprezentujících všechny hrany.

Výhody

• Extrémně úsporný pro ukládání hran
• Výhodný pro algoritmy, které procházejí všechny hrany (např. Kruskalův algoritmus)

Nevýhody

• Ověření existence hrany $O(m)$
• Složitější přístup k sousedům vrcholu

Příklad