Stromy

Strom je datová struktura, která reprezentuje hierarchické uspořádání dat. Skládá se z uzlů (vrcholů) a hran spojujících tyto uzly. Strom má vždy právě jeden kořenový uzel (root), ze kterého vedou hrany k ostatním uzlům. Mezi uzly platí vztah rodič–potomek (parent–child).

Pro každý strom musí platit, že je to graf, který:

• nesmí obsahovat cykly.
• mezi dvěma uzly existuje právě jedna cesta.

List je prvek stromu, který nemá potomky.

Využití stromů

Stromy se využívají v celé řadě oblastí informatiky a programování, například:

• Ukládání strukturovaných dat (například souborové systémy, XML/JSON dokumenty)
• Databázové indexy (například B-stromy, B+ stromy)
• Kompilátory (abstraktní syntaktické stromy)
• Vyhledávání a řazení dat
• Algoritmy pro směrování v sítích

Typy stromů

Existuje velké množství druhů stromů, lišících se svými vlastnostmi a účelem použití:

• Obecné (n-ární) stromy – uzel může mít libovolný počet potomků.
• Binární stromy – každý uzel má nejvýše dva potomky.
• Binární vyhledávací stromy (BST) – speciální binární stromy určené pro vyhledávání.
• Vyvážené stromy (například AVL, Red-Black) – binární vyhledávací stromy, které udržují vyváženou strukturu pro zajištění optimálnějšího vyhledávání.
• Heap (halda) – binární stromová struktura splňující haldové uspořádání.
• B-stromy, B+ stromy – používané v databázových systémech pro efektivní ukládání velkých objemů dat a následné dotazování se nad daty.

Význam B v B-stromech

Mohlo by se zdát, že B se u B-stromů znamená binární, ale to není pravda. Jedná se o balanced.

Binární stromy

Binární strom je strom, ve kterém každý uzel může mít maximálně dva potomky – levého a pravého.

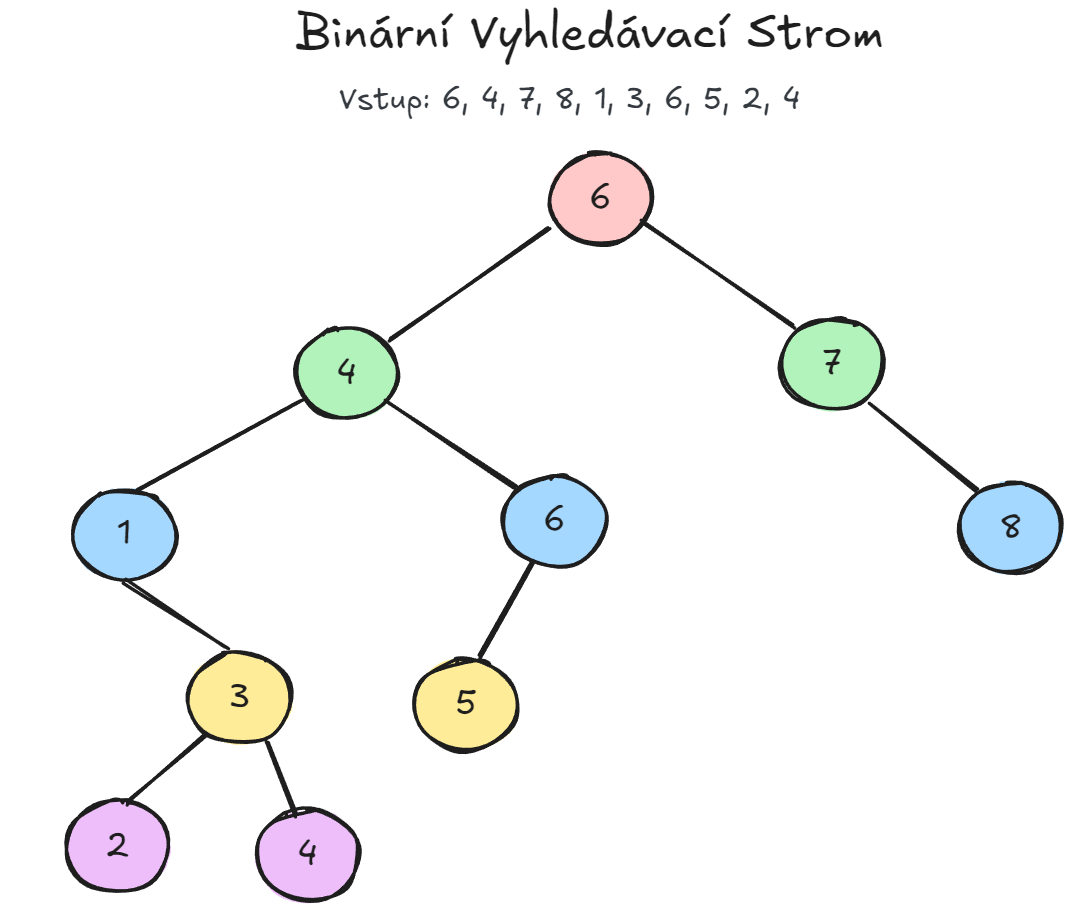
Binární vyhledávací strom (BST)

Binární vyhledávací strom (Binary Search Tree) je binární strom, který splňuje podmínku, že pro každý uzel platí:

• všechny uzly v levém podstromu obsahují hodnoty menší než hodnota v uzlu,
• všechny uzly v pravém podstromu obsahují hodnoty větší než hodnota v uzlu.

Výhodou BST je průměrná časová složitost operací $\mathcal{O}(logn)$, pokud je strom vyvážený. Nevýhodou je, že se strom automaticky nevyvažuje, tedy v extrémním případě (například při vkládání seřazených hodnot) může vzniknout „degenerovaný“ strom s časovou složitostí nalezení prvku $\mathcal{O}(n)$.

Operace v BST

• Vložení prvku – hodnota se vkládá do levého nebo pravého podstromu rekurzivně.
• Odstranění prvku
  • Pokud uzel
    • nemá potomky → odstraní se přímo
    • pokud má jednoho potomka → uzel se nahradí potomkem
    • pokud má dva potomky → nalezne se následník nebo předchůdce a hodnota se přepíše.
• Získání (vyhledání) prvku – vyhledává se podle vztahu menší/větší, což umožňuje rychlý průchod stromem.

Operace	Průměrná složitost	Nejhorší případ
Vložení	$\mathcal{O}(logn)$	$\mathcal{O}(n)$
Vyhledání	$\mathcal{O}(logn)$	$\mathcal{O}(n)$
Odstranění	$\mathcal{O}(logn)$	$\mathcal{O}(n)$

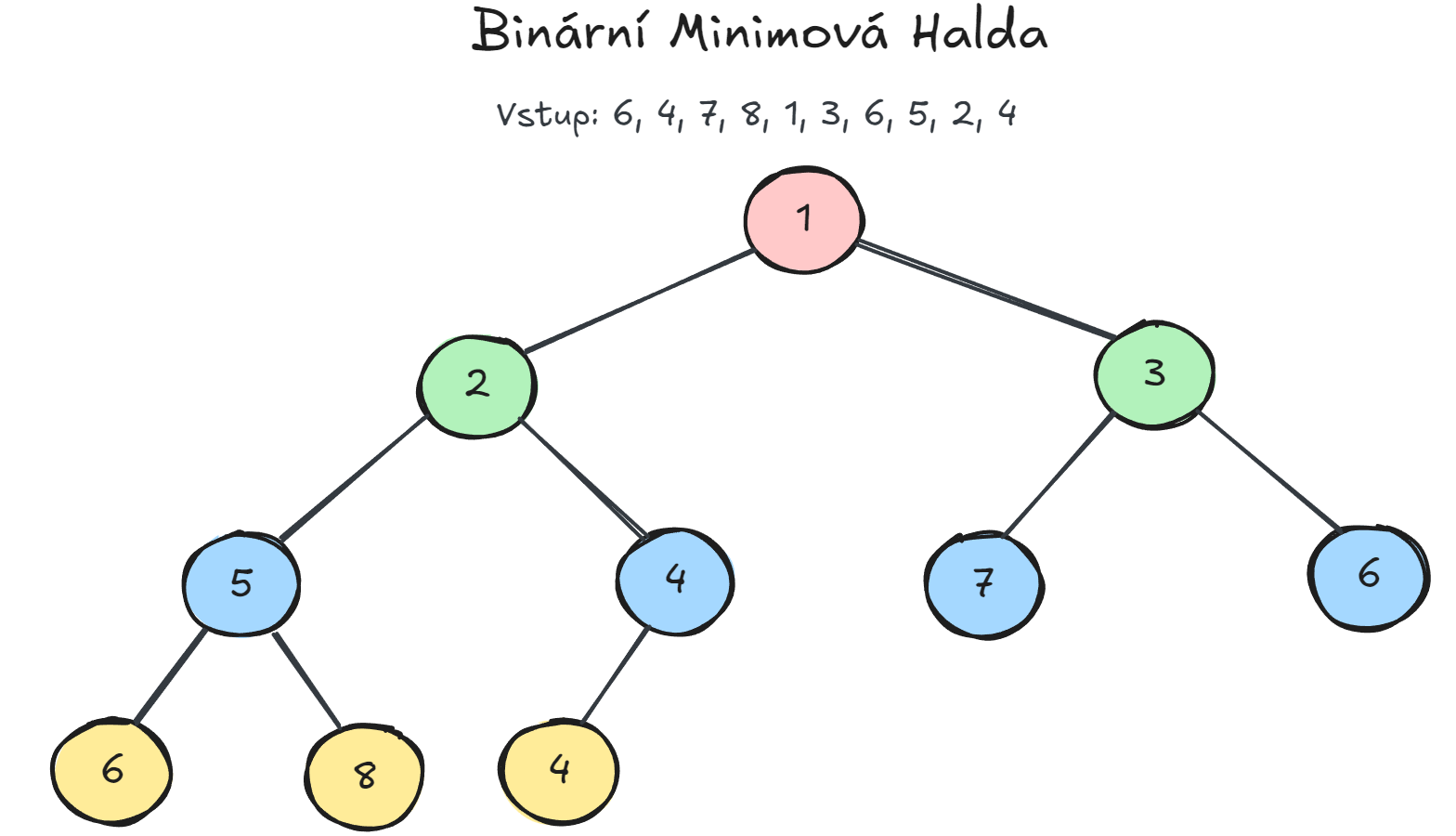
Binární halda

Binární halda (Binary Heap) je téměř úplný binární strom, který splňuje tzv. vlastnost haldy:

• u max-heapu platí, že hodnota rodiče je vždy větší nebo rovna hodnotám potomků,
• u min-heapu platí, že hodnota rodiče je menší nebo rovna hodnotám potomků.

Binární halda se využívá zejména pro implementaci prioritní fronty nebo algoritmů jako je heapsort.

Operace v binární haldě

• Vložení prvku – nový prvek se vloží na poslední volnou pozici a poté tzv. „vybublá“ nahoru, dokud není splněna vlastnost haldy.
• Odstranění prvku – u max-heapu se odstraní kořen, poslední prvek se přesune na kořenovou pozici a následně „propadá“ dolů, dokud není splněna vlastnost haldy.
• Získání min/max prvku – nalézá se vždy v kořeni pro min/max-heap.

Operace	Složitost
Vložení	$\mathcal{O}(logn)$
Odstranění max/min	$\mathcal{O}(logn)$
Přístup k max/min	$\mathcal{O}(1)$

Uložení do pole

Binární haldu lze mimo jiné uložit do jednorozměrného pole.

Platí následující vztahy:

• na indexu 0 je kořen
• levý potomek je na indexu $2i+1$, kde $i$ je index rodiče
• pravý potomek $2i+2$, kde $i$ je index rodiče